본 블로그 포스팅은 : 대학수학 College Mathemathics 3판 김남현 외 4명 공저 에서 일부 문제와 개념을 인용했음을 알립니다.
3.5 선형화
미시적인 부분에 한해서 그 함수를 직선으로 간주하고, 그것을 이용해서 함숫값을 추정하는 것을 선형화라고 한다.
함수를 직선으로 간주하기 위해서, 함수는 그 지점에서 미분이 가능해야한다.
예제 1번과 desmos를 이용해서 예시를 한번 들어보면 :
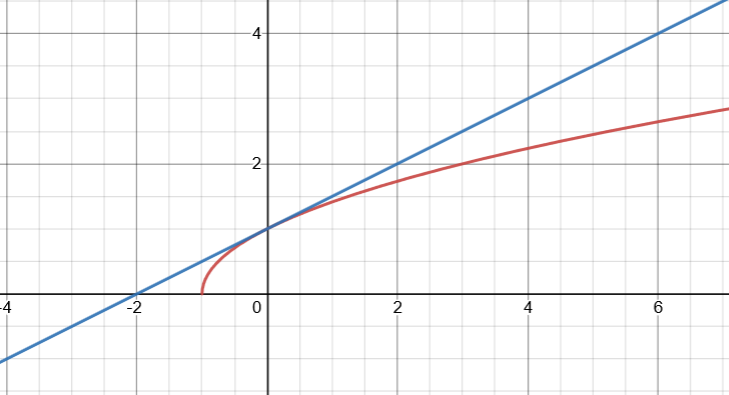
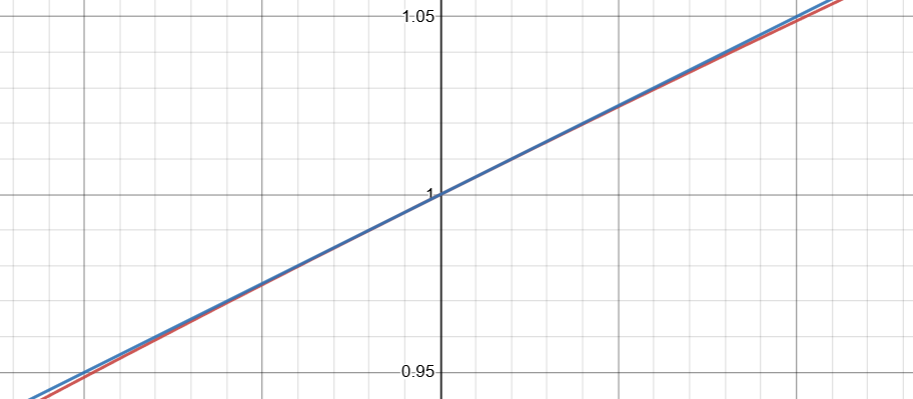
따라서 아주 근접한 곳에 한해서 선형화 된 함수를 실제 함수 대신 사용할 수 있다.
이러한 함수 $L$은, 본 함수 $f$와 접점의 $x$좌표, $x_0$에 대해서 다음과 같이 정의한다 :
$$ L(x) = f'(x_0)(x-x_0) + f(x_0) $$
이렇게 간단한 일차방정식 형태의 근사함수를 선형식 혹은 1차 근사식이라고 한다.
선형식은 뒤에 배울 뉴턴의 방법에 쓰이거나, 기존 함수의 변화량을 근사하는데 쓰인다. 여기서는 변화량을 어떻게 근사하는지를 알아 보도록 하자.
변화량에 대해서 이리저리 이야기하기 전에, 변화율은 익히 들어보았을 것이다. 순간 변화율은 미분계수이고, 평균 변화율도 $\Delta x$에 관해서 늘어난 $\Delta f$ 즉, $\Delta f / \Delta x$임을 알고 있을 것이다. 변화량은 평균 변화율의 $\Delta f$ = ($f$의 변화량), $\Delta x$ = ($x$의 변화량)들이므로, 평균 변화율을 이용한다면 언제나 정확한 변화량값을 알 수 있다.
$$ \Delta f = f(x_0 - \Delta x) - f(x_0) $$
$f$의 변화량은 위와 같다. 여기서 선형식을 이용해서 기존 함수를 근사해보자. $ L(x) = f'(x_0)(x-x_0) + f(x_0) $의 변화량 $\Delta L$을 구하면,
$$ \Delta L = L(x_0 + \Delta x) - L(x_0) = f(x_0) + f'(x_0) ((x_0 + \Delta x) - x_0) - f(x_0) = f'(x_0)\Delta x $$
이다. 전의 식에 비해서 훨씬 간단하다. $\Delta x \to 0$에 대해서는 $\Delta L$을 $\Delta f$대신 이용할 수 있으며, 이 경우에 $\Delta L$을 $df$라고 하며, $f$의 미분(differential)이라고 부른다.
$$ df = f'(x_0)dx $$
d를 쓰면 추정값을 나타내고, $\Delta$를 쓰면 실제 계산한 값을 나타낸다고 생각하면 된다.
'대학교과 > etc과목' 카테고리의 다른 글
| [건축용어 정리] - 예술과 건축 (0) | 2021.06.06 |
|---|---|
| [선사시대] 메소포타미아 - 예술과 건축 - 강의록 1 (0) | 2021.06.06 |
| 대학수학 - 역삼각함수와 쌍곡선함수 (0) | 2021.04.22 |
| 예술과 건축 - 영화 <About Time>과 건축물에 대해서. (0) | 2021.04.21 |
| 대학물리 - 1장 연습문제 풀어보기 3,8,15 (0) | 2021.04.05 |

